Article originally posted on Quantitative Trading blog by Dr. Ernest P. Chan
Much has been written about the Post-Earnings Announcement Drift (PEAD) strategy (see, for example, my book), but less was written about pre-earnings announcement strategies. That changed recently with the publication of two papers. Just as with PEAD, these pre-announcement strategies do not make use of any actual earnings numbers or even estimates. They are based entirely on announcement dates (expected or actual) and perhaps recent price movement.
The first one, by So and Wang 2014, suggests various simple mean reversion strategies for US stocks that enter into positions at the market close just before an expected announcement. Here is my paraphrase of one such strategies:
1) Suppose t is the expected earnings announcement date for a stock in the Russell 3000 index.
2) Compute the pre-announcement return from day t-4 to t-2 (counting trading days only).
3) Subtract a market index return over the same lookback period from the pre-announcement return, and call this market-adjusted return PAR.
4) Pick the 18 stocks with the best PAR and short them (with equal dollars) at the market close of t-1, liquidate at market close of t+1. Pick the 18 stocks with the worst PAR, and do the opposite. Hedge any net exposure with a market-index ETF or future.
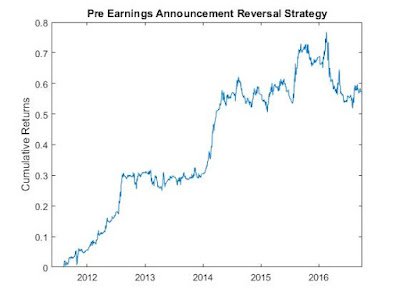
I backtested this strategy using Wall Street Horizon (WSH)'s expected earnings dates data, applying it to stocks in the Russell 3000 index, and hedging with IWV. I got a CAGR of 9.1% and a Sharpe ratio of 1 from 2011/08/03-2016/09/30. The equity curve is displayed below.
Note that WSH's data was used instead of Yahoo! Finance, Compustat, or even Thomson Reuters' I/B/E/S earnings data, because only WSH's data is "point-in-time". WSH captured the expected earnings announcement date on the day before the announcement, just as we would have if we were live trading. We did not use the actual announcement date as captured in most other data sources because we could not be sure if a company changed their expected announcement date on that same date. The actual announcement date can only be known with certainty after-the-fact, and therefore isn't point-in-time. If we were to run the same backtest using Yahoo! Finance's historical earnings data, the CAGR would have dropped to 6.8%, and the Sharpe ratio dropped to 0.8.
The notion that companies do change their expected announcement dates takes us to the second strategy, created by Ekaterina Kramarenko of Deltix's Quantitative Research Team. In her paper "An Automated Trading Strategy Using Earnings Date Movements from Wall Street Horizon", she describes the following strategy that explicitly makes use of such changes as a trading signal:
1) At the market close prior to the earnings announcement expected between the current close and the next day's open, compute deltaD which is the last change of the expected announcement date for the upcoming announcement, measured in calendar days. deltaD > 0 if the company moved the announcement date later, and deltaD < 0 if the company moved the announcement date earlier.
2) Also, at the same market close, compute deltaU which is the number of calendar days since the last change of the expected announcement date.
3) If deltaD < 0 and deltaU < 45, buy the stock at the market close and liquidate on next day's market open. If deltaD > 0 and deltaU >= 45, do the opposite.
The intuition behind this strategy is that if a company moves an expected announcement date earlier, especially if that happens close to the expected date, that is an indication of good news, and vice versa. Kramarenko found a CAGR of 14.95% and a Sharpe ratio of 2.08 by applying this strategy to SPX stocks from 2006/1/3 - 2015/9/2.
In order to reproduce this result, one needs to make sure that the capital allocation is based on the following formula: suppose the total buying power is M, and the number of trading signals at the market close is n, then the trading size per stock is M/5 if n <= 5, and is M/n if n > 5.
I backtested this strategy from 2011/8/3-2016/9/30 on a fixed SPX universe on 2011/7/5, and obtained CAGR=17.6% and Sharpe ratio of 0.6.
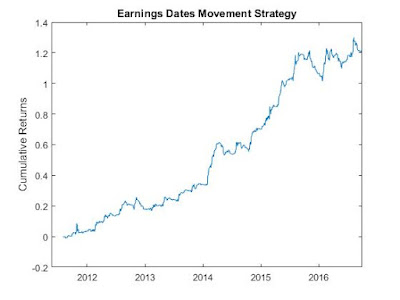
Backtesting this on Russell 3000 index universe of stocks yielded better results, with CAGR=17% and Sharpe ratio=1.9. Here, I adjust the trading size per stock to M/30 if n <=30, and to M/n if n > 30, given that the total number of stocks in Russell 3000 is about 6 times larger than that of SPX. The equity curve is displayed below:
Interestingly, a market neutral version of this strategy (using IWV to hedge any net exposure) does not improve the Sharpe ratio, but does significantly depressed the CAGR.
===
Acknowledgement: I thank Michael Raines at Wall Street Horizon for providing the historical point-in-time expected earning dates data for this research. Further, I thank Stuart Farr and Ekaterina Kramarenko at Deltix for providing me with a copy of their paper and explaining to me the nuances of their strategy.
_thumb.png)
_thumb.png)


_thumb.png)


_thumb.png)

_thumb.png)




